Znáte prolog?

Jednou jsem se zabýval matematikou a přemýšlel nad algoritmy řešící různé matematické úlohy. Některé jsou triviální a některé dají opravdu zabrat. Ono toto tvrzení není až tak pravda, většinou se ten algoritmus nějak do kupy dá, stačí zapomenout věnovat se nárokům na paměť. Ono dnešní počítače mají paměti dost, že .

Je hodně programovacích jazyků, mne zaujmul ale dotazovací jazyk Prolog. Výhodou jazyka Prolog je minimální počet příkazů, které je zapotřebí znát, vše ostatní si člověk vytváří pomocí faktů, pravidel a dotazů. Hlavní "doménou" Prologu je řešení úloh postavených na rekurzivním volání.

Například Euklidův algoritmus pro výpočet NSD. Znám dva způsoby, jak jej použít. První využívá celočíselného dělení, druhý využívá rozdílu. Pokud budeme chtít zapsat tento algoritmus pomocí rozdílu, vypadal by výsledek asi takto:

eu(X,X,X):-!.
eu(X,Y,NSD):-X<Y,!,eu(Y,X,NSD).
eu(X,Y,NSD):-X1 is X-Y,eu(X1,Y,NSD).

Přehledné že? Pomocí těchto tří řádku máme na světe algoritmus pro NSD využívající postupné odečítání menšího čísla od většího do doby, kdy se rovnají. Poté máme již výsledek.

Existují ale i náročnější úlohy, například Fibonacciho čísla. Čísla nacházející se ve Fibonacciho posloupnosti jsou někdy nazývána Fibonacciho čísla), kde každé číslo je součtem dvou předchozích.

Řešení v Prologu není zase těžké, když nad tím moc nepřemýšlíme:

f1(0,1).
f1(1,1).
f1(N,X):-N>1,N1 is N-1,N2 is N-2,f1(N1,X1),f1(N2,X2),X is X1 + X2.

Problém ovšem je ve větvení výpočtu jednotlivých čísel. Pokud by jsme si to rozkreslili, program postupuje následujícím způsobem pro číslo 15:

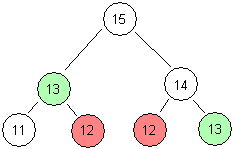
Z následujícího větvení je jasné, že se výpočet jednotlivých potřebných fibonacciho čísel provádí samostatně a z toho důvodu se počítají některá čísla několikrát. Pro malá čísla to poznat není, zkuste si tento algoritmus pustit s omezenou pamětí 64kB. Skončíte na čísle 15 (Local Stack Full), tedy 15 fibonacciho číslo je číslo 987.

Existuje elegantnější řešení:

f(N,X):-f(0,1,1,N,X).
f(N,X,Y,N,X):-!.
f(K,X,Y,N,V):-K1 is K+1,Z is X+Y,f(K1,Y,Z,N,V).

Tento algoritmus prochází čísla zleva, tedy vypočte vždy následující fibonacciho číslo za pomocí těch předcházejících. V těle prvního pravidla je zanesen následující fakt. Na pozici nuly dostaneme dané fibonacciho číslo, následuje fakt prvního a druhého čísla, N je naše zarážka a X je pomocná proměnná. 

Tento algoritmus dokáže vypočítat mnohonásobně větší číslo, konkrétně 1474 číslo fibonacciho posloupnosti, další pokus skončí přetečením.

| ?- f(1474,X).
X = 8.07763763215647E307

Pozn: číslo je uvedeno v semilogaritmickém tvaru.

Pokud se chtete blíže seznámit s Prologem, doporučuji "příručku" Programování v Prologu. Na stránce najdete vše potřebné.